El Teorema de Pitágoras establece que en un triángulo rectángulo el cuadrado de la longitud de la hipotenusa (el lado de mayor longitud del triángulo rectángulo) es igual a la suma de los cuadrados de las longitudes de los dos catetos (los dos lados menores del triángulo rectángulo: los que conforman el ángulo recto). Si un triángulo rectángulo tiene catetos de longitudes y , y la medida de la hipotenusa es , se establece que:
- Demostración
Sea el
triángulo rectángulo de catetos
a y
b e hipotenusa
c. Se trata de demostrar que el área del
cuadrado de lado
c es igual a la suma de las áreas de los cuadrados de lado
a y lado
b. Es decir:

Si añadimos tres triángulos iguales al original dentro del cuadrado de lado
c formando la figura mostrada en la imagen, obtenemos un cuadrado de menor tamaño. Se puede observar que el cuadrado resultante tiene efectivamente un lado de
b - a. Luego, el área de este cuadrado menor puede expresarse de la siguiente manera:
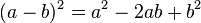
Ya que

.
Es evidente que el área del cuadrado de lado
c es la suma del área de los cuatro triángulos de altura
a y base
b que están dentro de él más el área del cuadrado menor:
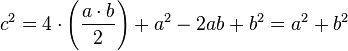
Con lo cual queda demostrado el teorema.
Demostraciones supuestas de Pitágoras
 Se cree que Pitágoras se basó en la semejanza de los triángulos ABC, AHC y BHC. La figura coloreada hace evidente el cumplimiento del teorema.
Se cree que Pitágoras se basó en la semejanza de los triángulos ABC, AHC y BHC. La figura coloreada hace evidente el cumplimiento del teorema.Se estima que se demostró el teorema mediante
semejanza de triángulos: sus lados homólogos son proporcionales.
[1]
Sea el triángulo ABC, rectángulo en C. El segmento CH es la altura relativa a la hipotenusa, en la que determina los segmentos
a’ y
b’, proyecciones en ella de los catetos
a y
b, respectivamente.
Los triángulos rectángulos ABC, AHC y BHC tienen sus tres bases iguales: todos tienen dos bases en común, y los ángulos agudos son iguales bien por ser comunes, bien por tener sus lados perpendiculares. En consecuencia dichos triángulos son semejantes.
- De la semejanza entre ABC y AHC:
y dos triangulos son semejantes si hay dos o más ángulos congruentes.
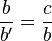

- De la semejanza entre ABC y BHC:

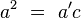
Los resultados obtenidos son el
teorema del cateto. Sumando:
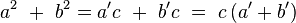
Pero
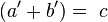
, por lo que finalmente resulta:

 La relación entre las superficies de dos figuras semejantes es igual al cuadrado de su razón de semejanza. En esto pudo haberse basado Pitágoras para demostrar su teorema
La relación entre las superficies de dos figuras semejantes es igual al cuadrado de su razón de semejanza. En esto pudo haberse basado Pitágoras para demostrar su teoremaPitágoras también pudo haber demostrado el teorema basándose en la relación entre las superficies de figuras semejantes.
Los triángulos PQR y PST son semejantes, de manera que:

siendo r la razón de semejanza entre dichos triángulos. Si ahora buscamos la relación entre sus superficies:
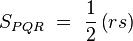
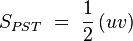
obtenemos después de simplificar que:
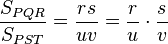
pero siendo

la razón de semejanza, está claro que:
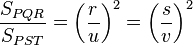
Es decir,
"la relación entre las superficies de dos figuras semejantes es igual al cuadrado de la razón de semejanza".
Aplicando ese principio a los triángulos rectángulos semejantes ACH y BCH tenemos que:
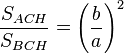
que de acuerdo con las propiedades de las proporciones nos da:
 (I)
(I)
y por la semejanza entre los triángulos ACH y ABC resulta que:

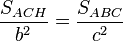
pero según
(I) 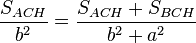
, así que:

y por lo tanto:
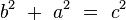
quedando demostrado el teorema de Pitágoras.
 Los cuadrados compuestos en el centro y a la derecha tienen áreas equivalentes. Quitándoles los triángulos el teorema de Pitágoras queda demostrado.
Los cuadrados compuestos en el centro y a la derecha tienen áreas equivalentes. Quitándoles los triángulos el teorema de Pitágoras queda demostrado.Es asimismo posible que Pitágoras hubiera obtenido una demostración gráfica del teorema.
Partiendo de la configuración inicial, con el triángulo rectángulo de lados
a,
b,
c, y los cuadrados correspondientes a catetos e hipotenusa –izquierda-, se construyen dos cuadrados diferentes:
- Uno de ellos –centro- está formado por los cuadrados de los catetos, más cuatro triángulos rectángulos iguales al triángulo inicial.
- El otro cuadrado –derecha- lo conforman los mismos cuatro triángulos, y el cuadrado de la hipotenusa.
Si a cada uno de estos cuadrados les quitamos los triángulos, evidentemente el área del cuadrado gris (
c2) equivale a la de los cuadrados amarillo y azul (
b2 + a2), habiéndose demostrado el teorema de Pitágoras.
 .
.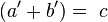 , por lo que finalmente resulta:
, por lo que finalmente resulta: la razón de semejanza, está claro que:
la razón de semejanza, está claro que: (I)
(I)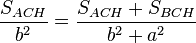 , así que:
, así que:
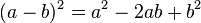
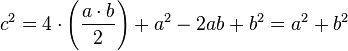

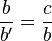


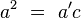
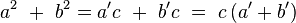


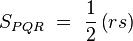
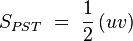
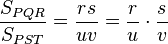
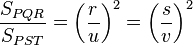
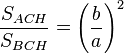

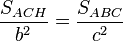

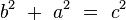

No hay comentarios:
Publicar un comentario